Vai jūs atceraties, kāds ir mērogs?

Lai varētu attēlotpapīra izstrādājumi, kas patiesībā nav ļoti "ērti" izmēri, cilvēki ir izveidojuši mērogu. Stingri sakot, tas izskaidro, kāpēc mērogs ir vajadzīgs.

Kad skolu mācību programma sāk atklāt apjoma jēdzienu

Pirmo reizi bērni saskaras ar šo vārdu laikāstudiju kartes un reljefa plāni. Skolotājs paskaidro, kāds ir mērogs, ko viņš parāda, izmantojot atlantu piemēru. Ir paskaidrots, ka jebkurš ģeogrāfiskais objekts ir tik liels, ka tā tēls dabiskajā izmērā būs grūti un neērti.

Cilvēki krāso platību samazinātā formā, betjo netika izmantotas precīzas attiecības. Tagad tas tiek darīts saprātīgi - katrai karti un līnijai, kas attēlota kartē, ir izmērs, kuru var reizināt ar noteiktu skaitu un uzzināt patieso garumu un platumu.

Mēroga reģistrēšana: pirmais lasīšanas veids

Mērogs tiek apzīmēts ar diviem numuriemcaur kolu. Pirmais cipars apzīmē izmēru vienības attēlā, otrajā norāda cik reālās vienības ciparī atbilst pirmajam skaitlim. Piemēram, ja plānā ir norādīta 1: 1000 skala, un vienības izmēri tiek norādīti centimetros, tad viens centimetrs skaitlī atbilst realitātei 1000 cm. Izrādās, kāds ir mērogs? Ar tās palīdzību jūs varat ne tikai samazināt dažus objektus grafiskajā plaknē, bet arī precīzi aprēķināt to reālo lielumu.

Otrais veids, kā uzrakstīt skalu: kas ir ērti?

Iepriekšējais veids, kā rakstīt skalu caur kolusauc par skaitlisku. Bet ir arī nosaukts mērogs. Viņa ieraksts ir šāds: 1 cm - 20 km. Izrādās, ka šādā veidā ir iespējams kompakti ierakstīt milzīgas svari, kas netiks izteikti ar numuriem ar vairākām nulles, ja situācija notiks, ja ir nepieciešams norādīt vairākus simtus kilometru vienā centimetrā. Tas ir uzreiz skaidrs, cik daudz, ko un ko. Šāds ieraksts ir intuitīvāks un intuitīvāks.

Raksturošana mērogojamībā: ko papildina iepriekš izpētīta koncepcija

Ar mēroga jēdzienu viņi saskaras ne tikaiģeogrāfiju, bet arī pētot šādu priekšmetu kā zīmējumu. Tie paši principi tiek izmantoti, lai pārstāvētu dažādus objektus. Bet ir būtiska atšķirība: šeit jēdziens par to, kāds ir mērogs, paplašinās arī tāpēc, ka ar tās palīdzību ir iespējams mazākās detaļas attēlot daudz plašāk. Ģeogrāfiskā situācijā tas tā nav, jo ģeogrāfijā nav tik maz objektu, ka ir nepieciešams tos palielināt. Kontinenti un kalni, upes un ezeri jebkurā gadījumā ir vairāk nekā A4 papīra loksnes vai pat A1.

Studējot zīmējumu, jūs varat izmantot skalu, lai lielākā formā attēlotu mazākās detaļas, piemēram, skrūvi vai skrūvi.

Tātad, kāpēc šajā gadījumā mums vajadzīga skala? Ar to palīdzību jūs varat ērtāk, skaidri un detalizēti attēlot nelielu elementu. Šajā gadījumā, notiek pretējs ierakstā: pirmais skaitlis ir lielāks par otro, un ierakstīt 100: 1 skanēs apmēram šādi: 100 vienības attēla Metrika atbilst vienas vienības faktisko lielumu.

Daži paskaidrojoši piemēri

Kāda ir skala, par ko tā parādāsVai ir mazāka objekta attēls, kas ir rezultāts papīra formātā? Atkal mums ir precīza saikne starp detaļas attēla izmēriem un reālo objektu. Atsaukt to pašu mērogu 100: 1. Izrādās, ka simts milimetros attēlā ir tikai viens milimetrs no reāla izmēra. Ja daļas platums ir 500 mm attēlā, tā reālais platums ir tikai 5 milimetri.

Ja mēs atcerosim pirmo lietu, tad attēlsuz liela objekta mazākās kopijas lapas skala no 1: 100 nozīmē, ka vienā milimetrā skaitlis satur 100 milimetrus patiesā lieluma. Kopā, ja objekta garums uz zīmējuma vai kartes ir 80 milimetri, patiesībā objekta garums būs 8000 milimetri. Skaidrs piemērs tam, kāds ir mērogs un kāds ir cilvēces ērtais izgudrojums.

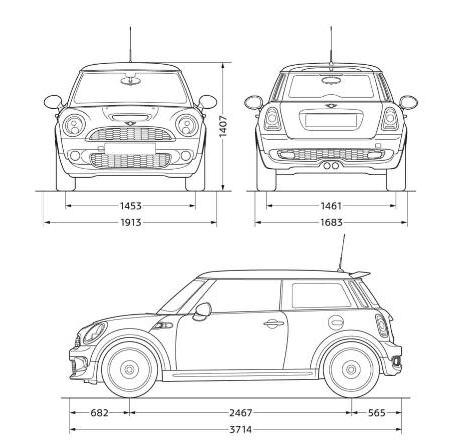
Galvenais skalas pielietojums ir vienlaicīgiAtcerieties, ka pirmais numurs attiecas uz attēlu, bet otrais - uz faktisko objektu izmēru. Lai nepieļautu neskaidrību, lai nostiprinātu šos pamatus skolās, tiek veiktas praktiskās ģeogrāfiskās nodarbības, lai bērni ar atlases palīdzību vairākas reizes izskaidro un aprēķinātu reālo objektu izmērus. Tas pats notiek arī zīmēšanas nodarbībās.

Apkopēsim rezultātus

Kāda ir skala? Atbilde uz šo jautājumu sastāv no trim punktiem, kas jums vienkārši jāatceras:

• Pirmkārt, skala ir nepieciešama, lai parādītu lielus objektus uz viegli uztveramas virsmas.
• Otrais ir tas, ka skala ir nepieciešama, lai attēlotu mazos lielāka izmēra objektus.
• Treškārt, mērogs ir vajadzīgs, lai varētu precīzi noteikt reāla objekta izmēru neatkarīgi no sākotnējās vērtības, mazs vai liels.
</ ul </ p>