Koordinātu līnija. Punkti uz koordinātu līnijas. Kā uzbūvēt koordinātu līniju

Sakot, ka jūs zināt, ka matemātika nav iespējama.ja jūs nezināt, kā veidot grafiku, attēlojiet nevienādības koordinātu līnijā, strādājiet ar koordinātu asīm. Zinātniskā vizuālā sastāvdaļa ir vitāli svarīga, jo bez skaidri redzamajiem piemēriem formulās un aprēķinos dažreiz var būt ļoti neskaidrs. Šajā rakstā mēs aplūkosim, kā strādāt ar koordinātu asīm, un uzzināsim, kā izveidot vienkāršas funkciju diagrammas.

Pieteikums

Koordinātu līnija ir vienkāršāko sugu pamatsdiagrammas, kuras students saskaras viņa izglītības ceļā. To lieto gandrīz katrā matemātiskajā tēmā: aprēķinot ātrumu un laiku, projektējot objektu lielumu un aprēķinot to platību, trigonometrijas laikā, strādājot ar sines un kosinēzēm.

Šādas taisnas līnijas galvenā vērtība ir redzamība. Tā kā matemātika ir zinātne, kurā ir nepieciešams augsts abstraktās domāšanas līmenis, grafiki palīdz objekta attēlojumā reālajā pasaulē. Kā viņš uzvedas? Kādā kosmosa vietā tas būs pēc dažām sekundēm, minūtēm, stundām? Ko jūs varat teikt par to salīdzinājumā ar citiem objektiem? Kādam ātrumam tas ir nejauši izvēlētā brīdī? Kā raksturot viņa kustību?

Un par ātrumu tas nav bez iemesla - tā ir viņaibieži rāda funkciju grafikus. Tie var arī parādīt temperatūras vai spiediena izmaiņas objektā, tā izmērus, orientāciju attiecībā pret horizontu. Tādējādi bieži vien ir nepieciešams izveidot koordinātu līniju fizikā.

Viendimensiju grafika

Ir daudzdimensiju jēdziens. Viendimensiju telpā tikai viens numurs ir pietiekams, lai noteiktu vietas atrašanās vietu. Tas ir tikai gadījumā ar koordinātu līnijas izmantošanu. Ja telpa ir divdimensiju, tad ir vajadzīgi divi skaitļi. Šāda veida diagrammas tiek izmantotas daudz biežāk, un nedaudz tālāk šajā rakstā mēs noteikti tos apsvērt.

Ko jūs varat redzēt ar punktiem uz ass, javiņa ir tikai viena? Jūs varat redzēt objekta lielumu, tā pozīciju kosmosā attiecībā uz dažiem "nulles", t.i., punktu, kas izvēlēts kā atskaites punkts.

Parametru maiņa laika gaitā nav redzama, jo visas norādes tiks parādītas konkrētā brīdī. Bet ar kaut ko, kas jums jāsāk! Tātad, sāksim darbu.

Kā izveidot koordinātu asi

Vispirms ir jāveic horizontāls darbslīnija - tā būs mūsu ass. Labajā pusē "asināt" to, lai tas izskatās kā bulta. Tādējādi mēs apzīmējam virzienu, kādā skaitļi palielināsies. Samazināšanas virzienā bultiņa parasti nav iestatīta. Tradicionāli ass ir vērsta uz labo pusi, tāpēc mēs vienkārši sekojam šim noteikumam.

Ievietojiet nulles atzīmi, kas būsparādīt koordinātu izcelsmi. Šī ir vieta, no kuras jūs rēķināties, neatkarīgi no tā, vai tas ir izmērs, svars, ātrums vai kaut kas cits. Papildus nullei mums vienmēr jānorāda ts dalīšanas cena, tas ir, jāievieš vienības standarts, saskaņā ar kuru mēs atdosim noteiktus daudzumus uz asi. Tas jādara, lai varētu atrast seguma garumu koordinātu līnijā.

Caur vienādu attālumu viens no otra mēs ieliekampunktus vai "iecirtumus" uz līnijas, un zem tiem mēs attiecīgi rakstīsim 1,2,3 un tā tālāk. Un tagad viss ir gatavs. Bet ar iegūto grafiku jums joprojām ir jāapgūst, kā strādāt.

Koordinātu līnijas punktu veidi

Īss ieskats mācību grāmatāsskaitļi kļūst skaidrs: punktus uz asi var krāsot vai nezāģēt. Vai jūs domājat, ka tas ir negadījums? Nav vispār! Nepārsvaru nevienlīdzībai tiek izmantots "cietais" punkts - apjoms, kas tiek nolasīts kā "lielāks vai vienāds ar". Ja ir nepieciešams stingri ierobežot intervālu (piemēram, "x" var ņemt vērtības no nulles uz vienu, bet to neiekļauj), mēs izmantojam "dobu" punktu, tas ir faktiski mazs aplis ass. Jāatzīmē, ka studentiem nepatīk stingra nevienlīdzība, jo viņiem ir grūtāk strādāt.

Atkarībā no tā, kuru punktu jūs izmantojatuz grafika, tiks izsaukta un izveidotie intervāli. Ja nevienlīdzība abās pusēs nav stingra, tad mēs iegūstam segmentu. Ja, no vienas puses, tas ir "atvērts", tad to sauc par pusi intervālu. Visbeidzot, ja taisnas līnijas daļa no divām pusēm ir ierobežota ar dobiem punktiem, to sauc par intervālu.

Lidmašīna

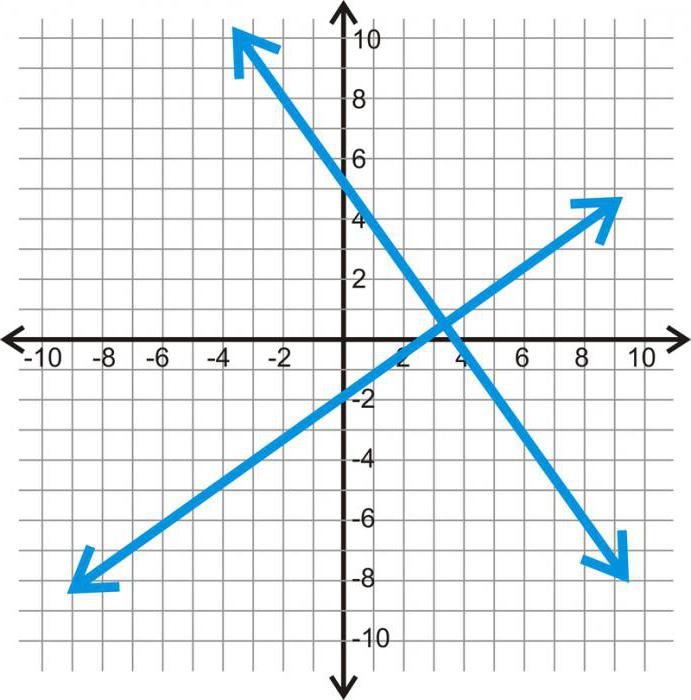
Izveidojot divas līnijas uz koordinātulidmašīna, mēs varam jau apsvērt funkciju grafikus. Piemēram, horizontālā līnija būs laika ass, un vertikālā līnija būs attālums. Un tagad mēs varam noteikt, kādā attālumā objekts tiks pārvarēts minūtē vai stundu ceļā. Tādējādi darbs ar plakni ļauj kontrolēt objekta stāvokli. Tas ir daudz interesantāk nekā statiskas valsts izpēte.

Vienkāršākais grafiks šādā plaknē ir taisna līnija, tā atspoguļo funkciju Y (X) = aX + b. Vai līnija ir saliekta? Tas nozīmē, ka objekts izmaina savas īpašības pētniecības procesā.

Iedomājieties, ka jūs stāvat uz ēkas jumta un turietizstieptajā rokā akmens. Kad jūs to atbrīvojat, tas atlaidīsies uz leju, sākot ar nulles ātrumu. Bet sekundē viņš pārvarēs 36 kilometrus stundā. Akmens turpinās paātrināties tālāk un vilkt to kustību grafikā, jums būs jāmaina tā ātrums vairākos punktos, ievietojot punktus uz asi atbilstošajās vietās.

Marķējumi uz horizontālās koordinātes līnijasnoklusējuma nosaukums ir X1, X2, X3 un vertikāli - attiecīgi Y1, Y2, Y3. Projektējot tos lidmašīnā un atrodot krustojumus, mēs atrodam izveidotā modeļa fragmentus. Apvienojot tos ar vienu rindiņu, mēs iegūstam funkciju grafiku. Krītošā akmens gadījumā kvadrātveida funkcija būs šāda: Y (X) = aX * X + bX + c.

Tuvināt

Protams, nav nepieciešams izstādīt blakussadalījumi ar tiešo vesels skaitļu vērtībām. Ja jūs apsverat gliemeža kustību, kas piebremzē ātrumu 0,03 metri minūtē, koordinātes taisnā vērtība tiek noteikta kā frakcija. Šajā gadījumā iestatiet sadales cenu par 0,01 metriem.

Īpaši ērti šādus rasējumus veikt piezīmjdatorākas būris - šeit jūs tūlīt varat redzēt, vai lapas ir pietiekami daudz vietas jūsu grafikam, vai jūs atstāsiet laukus. Tās spēks aprēķināt ir vienkāršs, jo šūnas platums šādā piezīmju grāmatiņā ir 0,5 centimetri. Tas bija nepieciešams - samazināja skaitli. No diagrammas mēroga izmaiņām tas nezaudēs un nemainīs tā īpašības.

Punkta un segmenta koordinātas

Kad mācība dod matemātisku problēmu, inTas var saturēt dažādu ģeometrisko skaitļu parametrus gan malu garuma, gan perimetra, apgabala un koordinātu veidā. Šajā gadījumā jums var būt nepieciešams izveidot skaitli un iegūt ar to saistītus datus. Rodas jautājums: kā atrast vajadzīgo informāciju par koordinātu līniju? Un kā veidot skaitli?

Piemēram, mēs runājam par punktu. Tad lielā burts parādīsies problēmas stāvoklī, un iekavās būs vairāki cipari, parasti divi (tas nozīmē, ka mēs tiksim ieskaitīti divdimensiju telpā). Ja iekavās ir trīs skaitļi, kas rakstīti ar semikolu vai komatu, tā ir trīsdimensiju telpa. Katra no vērtībām ir koordinātas uz attiecīgās ass: vispirms pa horizontāli (X), pēc tam vertikāli (Y).

Atcerieties, kā izveidot gabalu? Jūs to pārgāja pa ģeometriju. Ja ir divi punkti, tad starp tām var izdarīt taisnu līniju. To koordinātas ir norādītas iekavās, ja problēma parādās segmentā. Piemēram: A (15, 13) - B (1, 4). Lai izveidotu šādu līniju, jums jāatrod un atzīmējiet punktus koordinātu plaknē, un pēc tam pievienojiet tos. Tas ir viss!

Un, kā jūs zināt, daudzus daudzumus var zīmēt ar līnijas segmentiem. Problēma ir atrisināta.

Aprēķini

Pieņemsim, ka ir objekts, stāvoklisko raksturo divi skaitļi gar X asi: tā sākas punktā ar koordinātu (-3) un beidzas ar (+2). Ja mēs vēlamies uzzināt šī objekta garumu, tad mums ir jāatskaita no mazākā skaitļa. Ņemiet vērā, ka negatīvais skaitlis absorbē atņemšanas zīmi, jo "mīnus mīnus dod plus". Tātad, mēs pievienojam (2 + 3) un saņemam 5. Tas ir vajadzīgs rezultāts.

Cits piemērs: Mums tiek dota objekta gala punkts un garums, bet ne sākotnējais (un tas ir nepieciešams, lai to atrastu). Ļaujiet zināmā punkta pozīcijai (6), kā arī izpētītā objekta izmēram - (4). Atņemot garumu no galīgās koordinātes, mēs saņemam atbildi. Kopā: (6 - 4) = 2.

Negatīvie skaitļi

Parasti viņiem ir jādarbojasnegatīvās vērtības. Šajā gadījumā mēs ejam pa koordinātu asi pa kreisi. Piemēram, objekts 3 cm augsti peld ūdenī. Treškārt, viņš ir iegremdēts šķidrā veidā, divas trešdaļas ir gaisā. Tad, izvēloties ūdens virsmu kā asi, objekta virsmas aprēķināšanai mēs izmantojam divus elementālos numurus: objekta virsotnei ir koordinātas (+2) un apakšējā (-1) centimetra.

Nav grūti saprast, ka attiecībā uz yMēs esam izveidojuši četrus ceturtdaļas no koordinātu līnijas. Katram no viņiem ir savs numurs. Pirmajā (augšējā labajā) daļā būs punkti ar divām pozitīvām koordinātām, otrajā - pa kreisi no augšas - vērtības gar "x" ass būs negatīvas, un saskaņā ar "igrik" - pozitīvu. Trešais un ceturtais skaitlis tiek ieskaitīts pretēji pulksteņrādītāja kustības virzienam.

Svarīgs īpašums

Jūs zināt, ka taisni var iedomāties kābezgalīgs punktu kopums. Mēs varam apskatīt jebkuru vērtību daudzumu, cik vien mēs gribam katrā ass pusē, taču mēs neatbildēsimies ar atkārtotām. Tas šķiet naivs un saprotams, taču šis apgalvojums izriet no svarīga fakta: katram skaitlim ir viens un tikai viens punkts koordinātu līnijā.

Secinājums

Atcerieties, ka visas asis, formas un, ja iespējams,grafika jāveido saskaņā ar lineālu. Mērījumu vienības izgudroja ne nejaušība - radot kļūdu sagatavošanā, jūs riskējat redzēt, vai attēls nav bijis izskats.

Esi uzmanīgs un uzmanīgs ēkāgrafikus un aprēķinus. Tāpat kā jebkura zinātne, kas mācās skolā, matemātika mīl precizitāti. Pievienojiet nelielu piepūli, un labas atzīmes neaizņems ilgu laiku.