Maclaurin sērija un noteiktu funkciju sadalīšanās

Mācīšanās augstākajā matemātikā ir jāzina,ka virknes sēriju, kas pieder pie attiecīgās sērijas konverģences intervāla, summa ir diferencēta funkcija, kas ir nepārtraukta un bezgalīgi daudzkārt atšķirīga. Rodas jautājums: vai ir iespējams apgalvot, ka konkrētā patvaļīgā funkcija f (x) ir varas virknes summa? Tas ir, kādos apstākļos f-th f (x) var attēlot varas virkne? Šāda jautājuma nozīme ir tāda, ka aptuveni (f) (x) ir iespējams aizstāt ar vairāku pirmo varas jēdzienu summu summu, ti, polinomu. Šāda funkciju aizstāšana ar diezgan vienkāršu izteiksmi - polinomu - ir ērta arī dažu matemātiskās analīzes problēmu risināšanā, proti: integrāļu risināšanā, diferenciālo vienādojumu aprēķināšanā utt.

Ir pierādīts, ka par kādu f-ii f (x), kas atšķiras ar to atvasinājumi ar (n + 1) -th lai var aprēķināt, ieskaitot jaunāko tuvumā (alfa - R; x₀ + R) no punkta x = α, spēkā ir šāda formula:

Šī formula ir slavenā zinātnieka Brooke Taylor vārds. Sēriju, kas iegūta no iepriekšējā, sauc par Maclaurin sēriju:

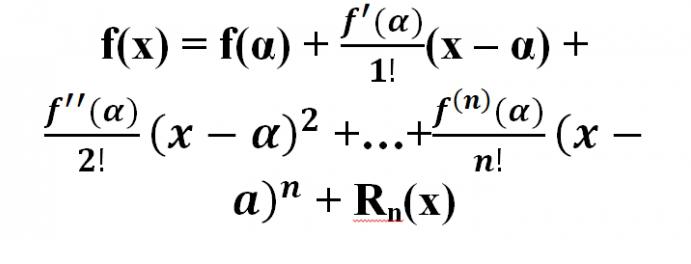
Noteikums, kas ļauj sadalīties Maclaurin sērijā:

1. Nosakiet pirmā, otrā, trešā pasūtījumu atvasinājumus.
2. Aprēķiniet, kādi atvasinājumi pie x = 0 ir vienādi ar.
3. Ierakstiet Maclaurin sēriju noteiktai funkcijai un pēc tam nosakiet tās konverģences intervālu.
4. Nosakiet intervālu (-R, R), kur pārējā Maclaurin formula

R_n(x) -> 0 kā n -> bezgalība. Gadījumā, ja tā pastāv, tajā funkcijai f (x) jāsakrīt ar Maclaurin sērijas summu.

Mēs tagad apsveram Maclaurin sēriju atsevišķām funkcijām.

1. Tādējādi pirmais ir f (x) = e^x. Protams, ka viņu raksturojums tā f-Ia ir iegūti dažādi pasūtījumu, un f^(k)(x) = e^x, kur k ir vienāds ar visiem dabiskajiem skaitļiem. Mēs aizvietojam x = 0. Mēs iegūstam f^(k)(0) = e⁰= 1, k = 1,2 ... Ņemot vērā iepriekš minēto, sērija e^x izskatīsies šādi:

2. Maclaurin sērija funkcijai f (x) = sin x. Tūlīt mēs paskaidrot, ka φ-th visiem nezināmiem būs atvasinājumi, turklāt f^"(x) = cos x = sin (x + n / 2), f^""(x) = -sin x = sin (x + 2 * n / 2) ..., f^(k)(x) = sin (x + k * n / 2), kur k ir vienāds ar jebkuru dabisko skaitli. Tas ir, veicot vienkāršus aprēķinus, mēs varam nonākt pie secinājuma, ka f (x) = sin x sērijai būs šāda forma:

3. Tagad mēs mēģinām izskatīt funkciju f (x) = cos x. Tam ir nejauša kārtojuma atvasinājumi visiem nezināmiem, un | f^(k)(x) | = cos (x + k * n / 2) | <= 1, k = 1,2 ... Atkal, izdarot noteiktus aprēķinus, iegūstam, ka f (x) = cos x sērija izskatās šādi:

Tātad, mēs esam uzskaitījuši vissvarīgākās funkcijas, kasvar sadalīties Maclaurin sērijās, bet dažām funkcijām tās papildina Taylor sērija. Tagad mēs tos uzskaitām. Ir arī vērts atzīmēt, ka Taylor un Maclaurin sērijas ir svarīga daļa no semināru risināt sērijas augstākajā matemātikā. Tātad, Taylor sērija.

1. Pirmais ir funkciju f (x) = ln (1 + x) sērija. Tāpat kā iepriekšējos piemēros, konkrētam f (x) = ln (1 + x) mēs varam pievienot sēriju, izmantojot Maclaurin sērijas vispārējo formu. Tomēr šīs funkcijas Maclaurin sērijas var iegūt daudz vienkāršāk. Dažu ģeometrisko sēriju integrēšana, mēs iegūstam šādu parauga f (x) = ln (1 + x) sēriju:

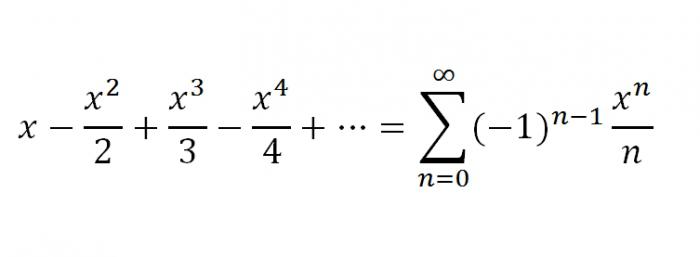
2. Un otrais, kas būs galīgais mūsu darbā, būs sērija f (x) = arctg x. X, kas pieder intervālam [-1; 1], ekspansija ir derīga:

Tas ir viss. Šajā rakstā tika aplūkotas visbiežāk lietotās Taylor un Maclaurin sērijas augstākās matemātikas, it īpaši ekonomikas un tehnikas universitātēs.